１．目的
　Y-デルタ結線においては、1次と2次とで位相差30°があることは知られている。
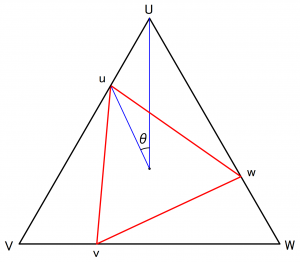
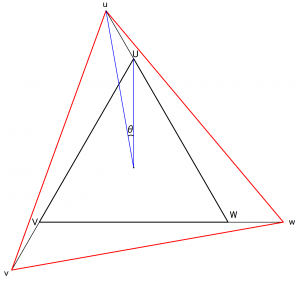
　デルタ-デルタ結線において、内接デルタ及び辺延びデルタ結線時の位相差（θ）を確認する。

　　　　　　　　　　内接デルタ結線　　　　　　　　　　　　　　　　　辺延びデルタ結線
　　 　　　　　

２．計算結果
　1次電圧を100Vとして2次電圧を振った時の位相差（θ）を示す。計算式の導き方は４項を参照。
　なお、内接デルタでは電圧を半分以下にすることはできないため、50Vまでのデータとなっている。

内接デルタ 辺延びデルタ
計算式 電圧比 = \displaystyle \frac{1}{2\cdot\sin(150-\theta)} 計算式 電圧比 = \displaystyle \frac{1}{2\cdot\sin(30-\theta)}
電圧[V]位相差[°] 電圧[V]位相差[°]
1000 1000
903.7 1103.0
808.7 1205.4
7015.6 1307.4
6026.4 1409.1
5060.0 15010.5
16011.8
17012.9
18013.9
19014.7
20015.5

３．結論
　内接デルタの位相差は、辺延びデルタより大きく、最大で60°となる。
　一般的な電圧タップ（±20%）での位相差は、10°以下であり、Ｙ－デルタ結線の位相差より小さい。
　辺延びデルタの最大位相差は計算式上30°となることがわかった。
　参考までに、内接デルタ及び辺延びデルタの巻数比計算方法を導き、その検証を行った。
　この内容については５項に示す。

４．位相差計算式
（１）内接デルタ結線
　　元のデルタ結線（黒△）と内接デルタ結線（赤△）との位相差θを求める。
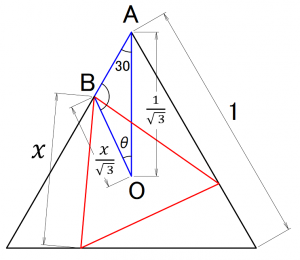　　元のデルタ結線の電圧を１として、内接デルタ結線の電圧をχとする。
　　三角形ABO（青△）を見た時、（Oは正三角形の重心）
　　　AO= \displaystyle \frac{1}{\sqrt{3}} , BO= \displaystyle \frac{x}{\sqrt{3}} , ∠ABO = 180 – 30 -θ = 150-θ　となる。
　　ここで、正弦定理　 \displaystyle \frac{a}{\sin(A)} = \frac{b}{\sin(B)}から
　　　 \displaystyle \frac{\frac{x}{\sqrt{3}}}{\sin(30)} = \frac{\frac{1}{\sqrt{3}}}{\sin(150-\theta)}
　　これを解いて
　　　 \displaystyle x=\frac{1}{2\cdot\sin(150-\theta)}
　　この式から逆算で位相差θを算出する。

（２）辺延びデルタ結線
　　元のデルタ結線（黒△）と辺延びデルタ結線（赤△）との位相差θを求める。
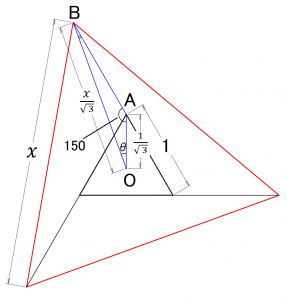　　元のデルタ結線の電圧を１として、辺延びデルタ結線の電圧をχとする。
　　三角形ABO（青△）を見た時、（Oは正三角形の重心）
　　　AO= \displaystyle \frac{1}{\sqrt{3}} , BO= \displaystyle \frac{x}{\sqrt{3}} , ∠ABO = 180-150-θ = 30-θ　となる。
　　ここで、正弦定理　 \displaystyle \frac{a}{\sin(A)} = \frac{b}{\sin(B)}から
　　　 \displaystyle \frac{\frac{x}{\sqrt{3}}}{\sin(150)} = \frac{\frac{1}{\sqrt{3}}}{\sin(30-\theta)}
　　これを解いて
　　　 \displaystyle x=\frac{1}{2\cdot\sin(30-\theta)}
　　この式から逆算で位相差θを算出する。

５．巻数計算式と、その検証
（１）内接デルタ結線
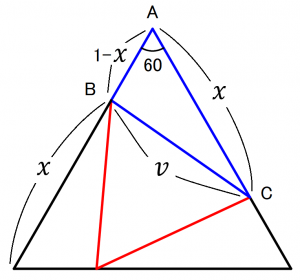　　元となる巻線数を1とした時、タップ電圧比がνとなる巻数χを求める。
　　余弦定理　 \displaystyle c^{2} = a^{2} + b^{2} - 2ab\cdot\cos(\theta) より
　　三角形ABC（青△）を見た時、
　　　 \displaystyle v^{2} = (1-x)^{2} + x^{2} - 2(1-x)x\cdot\cos(60) \displaystyle = 3x^{2} - 3x + 1
　　これを解いて、
　　　 \displaystyle x = \frac{1}{2} + \frac{1}{6}\sqrt{12v^{2} - 3}

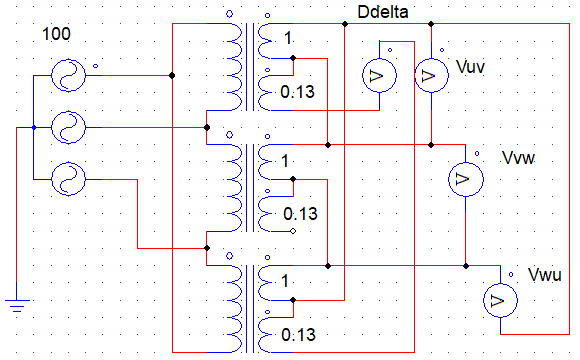
　　例）タップ電圧を0.8とする場合の巻数の比は上式より0.86となる。
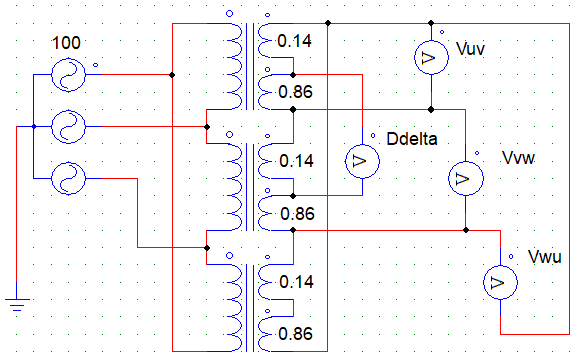
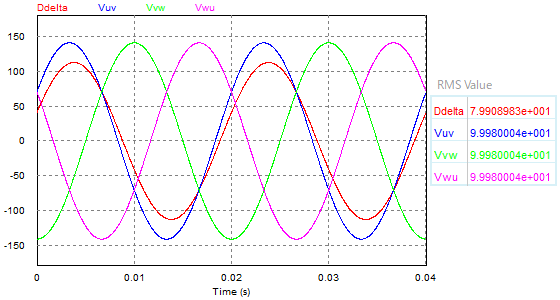
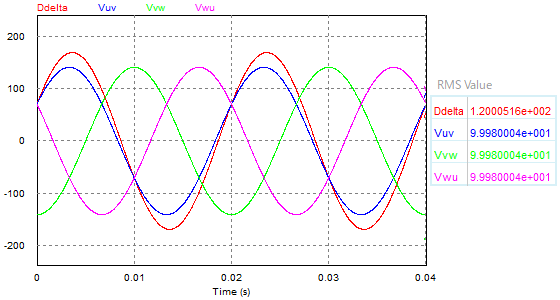
　　検証結果：ｼﾐｭﾚｰｼｮﾝの結果、100Vに対して約80Vが得られた。

　＜シミュレーション回路＞
　
　＜シミュレーション結果＞
　

（２）辺延びデルタ結線
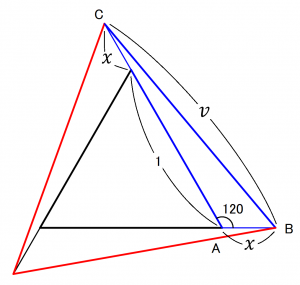　　元となる巻線数を1とした時、タップ電圧比がνとなる巻数χを求める。
　　余弦定理　 \displaystyle c^{2} = a^{2} + b^{2} - 2ab\cdot\cos(\theta) より
　　三角形ABC（青△）を見た時、
　　　 \displaystyle v^{2} = (1+x)^{2} + x^{2} - 2(1+x)x\cdot\cos(120) \displaystyle = 3x^{2} + 3x + 1
　　これを解いて、
　　　 \displaystyle x = -\frac{1}{2} + \frac{1}{6}\sqrt{12v^{2} - 3}

　　例）タップ電圧を1.2とする場合の追加巻数の比は上式より0.13となる。
　　検証結果：ｼﾐｭﾚｰｼｮﾝの結果、100Vに対して約120Vが得られた。

　＜シミュレーション回路＞
　
　＜シミュレーション結果＞