VI法によるリアクトルのインダクタンス(以降L値と記す)の測定方法を紹介します。
あわせて、他の測定方法での計測結果と比較し考察を行いました。
1.リアクトルのL値を求めるための算出式
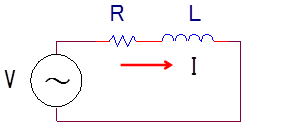
リアクトルは抵抗分とリアクトル分を持っているので、これをRL直列回路(図1)として考える。
この回路に正弦波交流電圧を印加した場合の電流を i=Isin(ωt)とすると、
(1)抵抗Rの両端電圧:VR = RIsin(ωt)
(2)リアクトルLの両端電圧:VL = ωLIsin(ωt+90°)
(3)合成電圧vは、
・電流に比べてφ=tan-1(ωL/R)だけ位相が進む形となり
・RとLの合成インピーダンスZは、
から、
v = Vsin(ωt+φ)となる。(ここで、V=ZI)
図.1
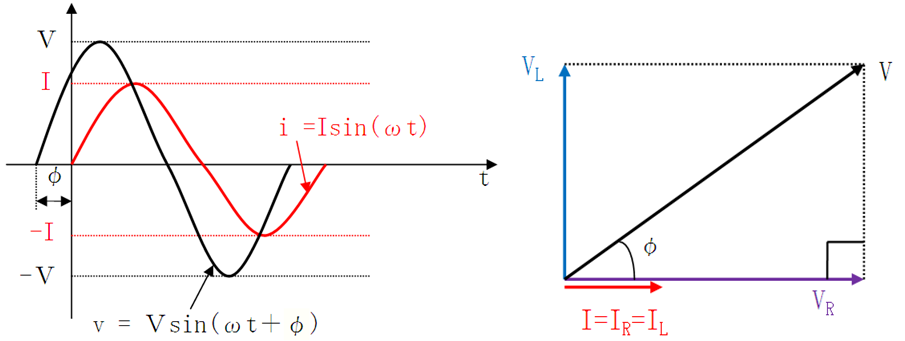
図.2 図.3
(4)ベクトル図より三角形のピタゴラスの定理を用いLの算出式が導かれる。
V2 = VR2 + VL2
V2 = (RI)2 + (ωLI)2 (ここでω= 2πf) よりL値は、
・・・・【式1】
2.VI法によるL値の測定
<測定方法>
(1)リアクトルの直流抵抗Rを事前に測定する。
(2)既知の周波数f,正弦波電圧V,その時の電流I(但し歪なきこと)を測定する。
(3)【式1】によりL値を算出する。
<測定結果>
試験リアクトル:TR-AF0366(0.2mH-40A)
周波数:60Hz
| 項目 | 記号 | 計測値 | 計測器 |
| 直流抵抗 | R | 8.975mΩ | ミリオームテスター |
| 電圧 | V | 4.205V | DMM |
| 電流 | I | 40.3A | クランプメータ |
3.電力計によるL値算出
<測定方法>
電力計では、皮相電力、有効電力、無効電力などをそれぞれ計測することができる。
ここで、有効電力からRを、無効電力からLを求めることができる。
(1)皮相電力:S=V×I[VA]
(2)有効電力:P=V×I×cosφ[W] = R×I2 より抵抗分は、
・・・・【式2】
(3)無効電力:Q=V×I×sinφ[Var] = ωL×I2 よりL分は、
・・・・【式3】
<測定結果>
試験リアクトル:TR-AF0366(0.2mH-40A)
周波数:60Hz
計測器:デジタルパワーメータ
| 項目 | 記号 | 計測値 |
| 電圧 | V | 4.31V |
| 電流 | I | 40.48A |
| 皮相電力 | S | 174.4VA |
| 有効電力 | P | 24.6W |
| 無効電力 | Q | 172.7Var |
リアクトルの直流抵抗分は、【式2】より
L値は、【式3】より
4.インピーダンス・アナライザによる測定
計測器:LFインピーダンス・アナライザ 4192A(HP)
試験リアクトル: TR-AF0366(0.2mH -40A)
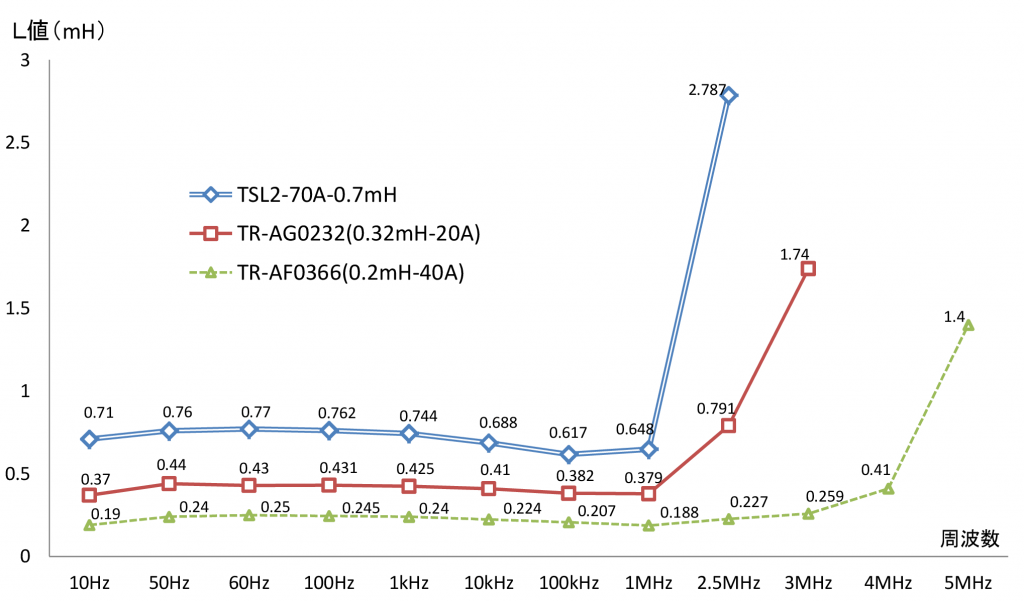
TSL2-70A-0.7mH(直列配線) ・・・参考データ
TR-AG0232(0.32mH-20A) ・・・参考データ
<測定結果>
5.結論
VI法による測定結果、および他の方法での測定結果をまとめると、
| 測定方法 | インダクタンス値(mH) | 直流抵抗値(mΩ) |
| VI法 | 0.2757 | 8.98 |
| 電力計法 | 0.2796 | 15.01 |
| インピーダンス・アナライザ | 0.25 | - |
VI法によりL値を計測できることがわかる。
ただし、鉄損が大きい場合は、値がずれるので注意が必要である。
6.考察
①インピーダンス・アナライザによる測定結果とVI法や電力計との差が大きい。
これは、インピーダンス・アナライザは実際に定格電流を流さずに測定しているため、
鉄心の特性などが実動作時と異なる為である。L値を測る場合は、実動作に近い状態で測る必要がある。
②周波数によりL値が変わるのは、容量成分など他のインピーダンスの影響によるものと考える。
特に高い周波数で、見かけ上L値が上昇するのは、容量成分とLによる共振のためである。









 ←投稿動画一覧
←投稿動画一覧
