１．目的
　スコット結線変圧器・逆V結線変圧器において、入力電圧の相バランスが崩れた時の出力電圧変動を確認する。

２．計算結果
　UVW相の入力電圧がそれぞれ±5%変動した時の計算結果を下記に示す。計算式は４項を参照。

入力電圧変動 出力電圧変動
逆V結線 スコット結線
UVVWWU uv出力T座出力M座出力直列接続
0%0%0% 0.0% 0.0% 0.0% 0.0%
0%0%+5% -1.7% +3.4% 0.0% -1.3%
0%0%-5% +1.6% -3.3% 0.0% +1.2%
0%+5%0% +3.4% +3.4% 0.0% +4.6%
0%+5%+5% +1.7% +6.6% 0.0% +3.4%
0%+5%-5% +4.9% +0.2% 0.0% +5.7%
0%-5%0% -3.3% -3.3% 0.0% -4.5%
0%-5%+5% -5.1% +0.2% 0.0% -5.9%
0%-5%-5% -1.6% -6.7% 0.0% -3.3%
+5%0%0% +3.4% -1.7% +5.0% +1.7%
+5%0%+5% +1.7% +1.7% +5.0% +0.5%
+5%0%-5% +4.9% -5.1% +5.0% +2.9%
+5%+5%0% +6.6% +1.7% +5.0% +6.2%
+5%+5%+5% +5.0% +5.0% +5.0% +5.0%
+5%+5%-5% +8.1% -1.6% +5.0% +7.3%
+5%-5%0% +0.2% -5.1% +5.0% -2.8%
+5%-5%+5% -1.6% -1.6% +5.0% -4.1%
+5%-5%-5% +1.8% -8.6% +5.0% -1.6%
-5%0%0% -3.3% +1.6% -5.0% -1.6%
-5%0%+5% -5.1% +4.9% -5.0% -2.9%
-5%0%-5% -1.6% -1.6% -5.0% -0.4%
-5%+5%0% +0.2% +4.9% -5.0% +3.0%
-5%+5%+5% -1.6% +8.1% -5.0% +1.8%
-5%+5%-5% +1.8% +1.8% -5.0% +4.1%
-5%-5%0% -6.7% -1.6% -5.0% -6.3%
-5%-5%+5% -8.6% +1.8% -5.0% -7.6%
-5%-5%-5% -5.0% -5.0% -5.0% -5.0%

３．結論
　スコット・逆V結線とも入力電圧±5%の変動に対し、規定の出力電圧に対して最大±8%程度の変動となることが分かった。また、スコット結線で直列接続した場合の出力変動が小さいことも分かった。

４．計算式
【スコット結線変圧器の出力電圧】
　
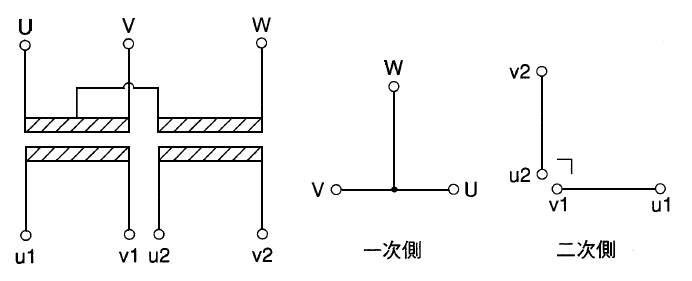
　　　　　　　回路図　　　　　　　　　　　　　　　　　ベクトル図

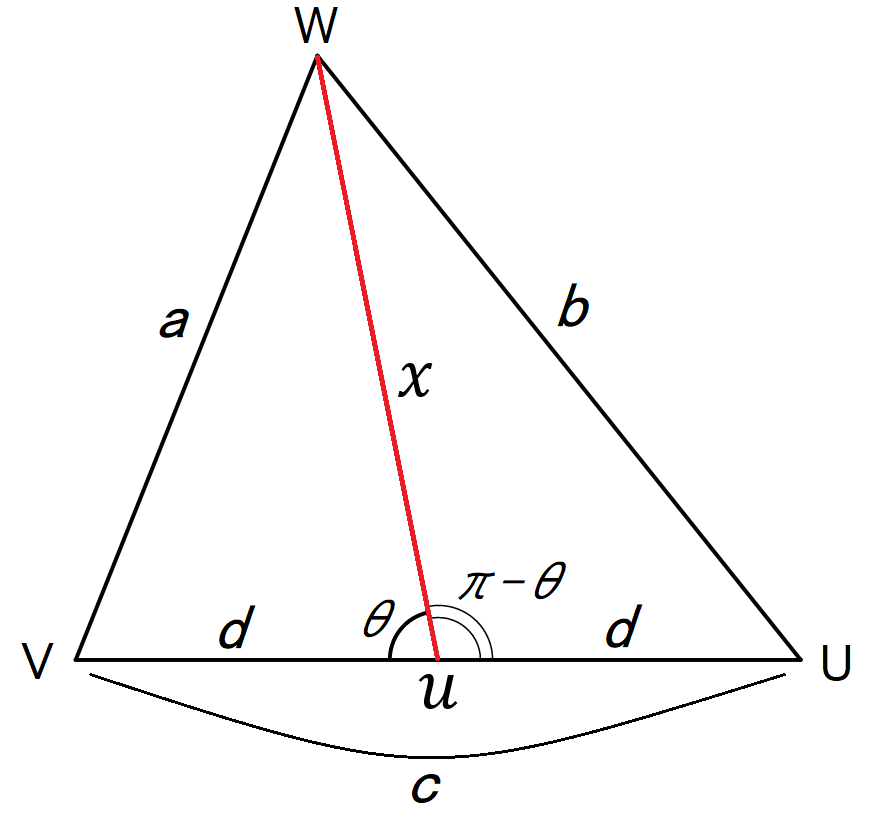
T座の電圧χはUVの中点uからWへの電圧（ \displaystyle \overrightarrow{uW}）となる。 \displaystyle d = \frac{1}{2}cとして、
⊿uVWをみたとき、余弦定理より、
　　　 \displaystyle a^{2} = x^{2} + d^{2} - 2xd\cos(\theta)　　　　・・・(1)
⊿uWUをみたとき、余弦定理より、
　　　 \displaystyle b^{2} = x^{2} + d^{2} - 2xd\cos(\pi-\theta)
ここで、 \displaystyle \cos(\pi-\theta) = -\cos(\theta)　より
　　　 \displaystyle b^{2} = x^{2} + d^{2} + 2xd\cos(\theta)　　　　・・・(2)
(1)式と(2)式の両辺を足して、
　　　 \displaystyle a^{2} + b^{2} = 2x^{2} + 2d^{2}
ここから、
　　　 \displaystyle x^{2} = \frac{1}{2}(a^{2} + b^{2} -2d^{2})
ここに、 \displaystyle d = \frac{1}{2}c　を代入してχを求める。
相間電圧VW, WU, UVをa,b,cとした時の出力電圧χは下記となる。
　　　 \displaystyle x = \sqrt{\frac{1}{2}(a^{2} + b^{2} -\frac{1}{2}c^{2})}　　　　・・・(3)
　　　　　 \displaystyle =\frac{1}{2}\sqrt{2(a^{2} + b^{2})-c^{2}}
なお、M座の電圧はUV間電圧に比例した値となる。

【スコット結線変圧器の直列接続出力電圧】
　

スコット変圧器では、通常T座とM座の出力電圧を同じであるので、直列接続する場合は、
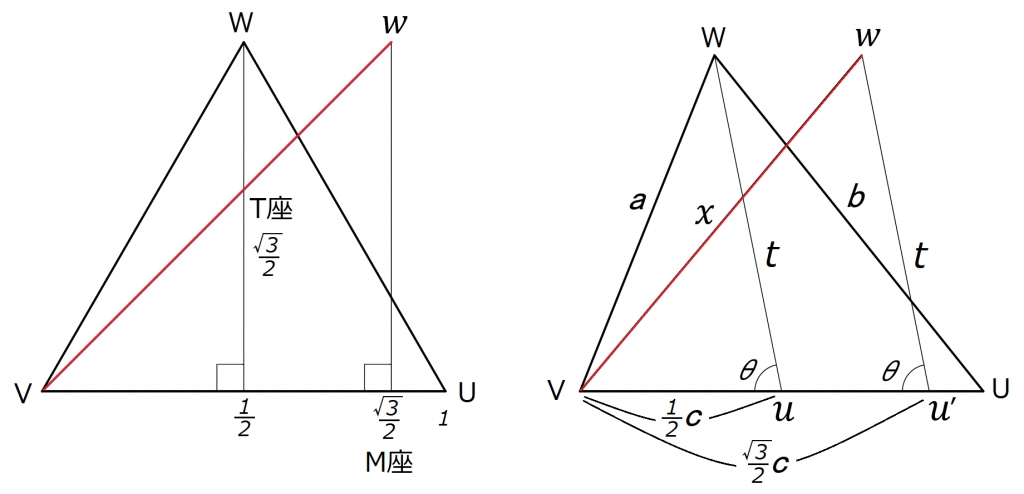
M座の出力電圧を単純に \displaystyle \frac{\sqrt{3}}{2}し、T座とM座の電圧を同じにしてVv間の電圧を求める。（上左図）
上右図で、⊿uVWをみたとき、余弦定理より、
　　　 \displaystyle a^{2} = (\frac{1}{2}c)^{2} + t^{2} - 2\cdot\frac{1}{2}ct\cos(\theta)
　　　 \displaystyle ct\cos(\theta) = \frac{1}{4}c^{2} + t^{2} - a^{2}　　　　・・・(4)
ここで、 \displaystyle t^{2}　は(3)式より、
　　　 \displaystyle t^{2} = \frac{1}{2}a^{2} + \frac{1}{2}b^{2} - \frac{1}{4}c^{2}　　　　　　・・・(5)
⊿u’Vwをみたとき、余弦定理より、
　　　 \displaystyle x^{2} = (\frac{\sqrt{3}}{2}c)^{2} + t^{2} - 2\cdot\frac{\sqrt{3}}{2}ct\cos(\theta)
ここに(4)式を代入して、
　　　 \displaystyle x^{2} = (\frac{3}{4}c^{2} + t^{2} - \sqrt{3}(\frac{1}{4}c^{2} + t^{2} - a^{2})
ここに(5)式を代入して展開すると、
　　　 \displaystyle x^{2} = \frac{3}{4}c^{2} + \frac{1}{2}a^{2} + \frac{1}{2}b^{2} - \frac{1}{4}c^{2} - (\frac{\sqrt{3}}{4}c^{2} + \frac{\sqrt{3}}{2}a^{2} + \frac{\sqrt{3}}{2}b^{2} - \frac{\sqrt{3}}{4}c^{2}- \sqrt{3}a^{2})
　　　　　 \displaystyle =(\frac{1}{2}-\frac{\sqrt{3}}{2}+\sqrt{3})a^{2}+(\frac{1}{2}-\frac{\sqrt{3}}{2})b^{2}+(\frac{3}{4}- \frac{1}{4}- \frac{\sqrt{3}}{4} +\frac{\sqrt{3}}{4})c^{2}
　　　　　 \displaystyle =(\frac{1+\sqrt{3}}{2})a^{2}+(\frac{1-\sqrt{3}}{2})b^{2}+\frac{1}{2}c^{2}
　　　 \displaystyle x =\sqrt{(\frac{1+\sqrt{3}}{2})a^{2}+(\frac{1-\sqrt{3}}{2})b^{2}+\frac{1}{2}c^{2}}　となる。

【逆V結線変圧器の出力電圧】
　

　　　　　　回路図　　　　　　　　　　　　　　　　　　ベクトル図

出力電圧χは \displaystyle \overrightarrow{UV} + \overrightarrow{WV} = \overrightarrow{Uv}　となる。
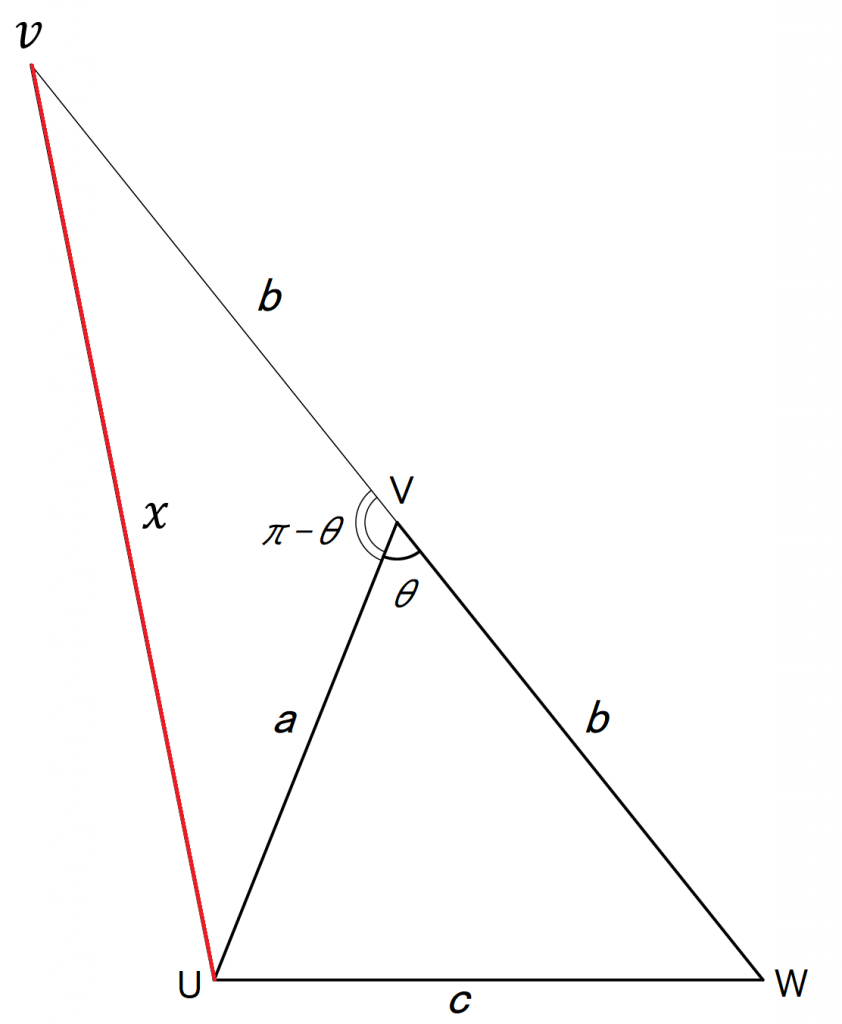
⊿UVWをみたとき、余弦定理より、
　　　 \displaystyle c^{2} = a^{2} + b^{2} - 2ab\cos(\theta)
　　　 \displaystyle \cos(\theta) = \frac{1}{2ab}(a^{2} + b^{2} - c^{2})　　　　　・・・(6)
⊿UVvをみたとき、余弦定理より、
　　　 \displaystyle x^{2} = a^{2} + b^{2} - 2ab\cos(\pi-\theta)
ここで \displaystyle \cos(\pi-\theta) = -\cos(\theta)　と(6)式より
　　　 \displaystyle x^{2} = a^{2} + b^{2} +(a^{2} + b^{2} -c^{2})
　　　　 \displaystyle = 2a^{2} + 2b^{2} - c^{2}
相間電圧UV,VW,WUをa,b,cとした時の出力電圧χは下記となる。
　　　 \displaystyle x =\sqrt{2(a^{2} + b^{2})-c^{2}}